广义表和二叉树的性质
0x01 广义表的定义
广义表是n(n>=0)个元素的有限序列,其中每一个元素或者是原子,或者是一个广义表。
广义表通常记为
1 | LS = (a1,a2,...,an) |
其中LS为表名,n为表的长度,每一个ai为表的元素
习惯上用大写字母表示广义表,小写字母表示原子
表头:若LS非空,则其中第一个元素a1就是表头,记为
1 | head(LS) = a1 |
表头可以是原子也可以是子表
表尾:除表头之外的其他元素组成的表
1 | tail(LS) = (a2,...,an) |
表尾表示最后一个元素,而是一个子表
0x02 广义表的性质
广义表中的数据有相对次序,一个直接前驱和一个直接后继
广义表的长度定义位最外层所包含的元素的个数
广义表的深度定义为该广义表展开后所含括号的重数
广义表可以为其他广义表共享
广义表可以是一个递归的表,递归表的深度是无穷值
广义表是多层次结构,可以用图形象地表示
0x03 树的定义
树(Tree) 是n (n≥0) 个结点的有限集。
若n=0,称为空树
若n>0,则它满足如下两个条件:
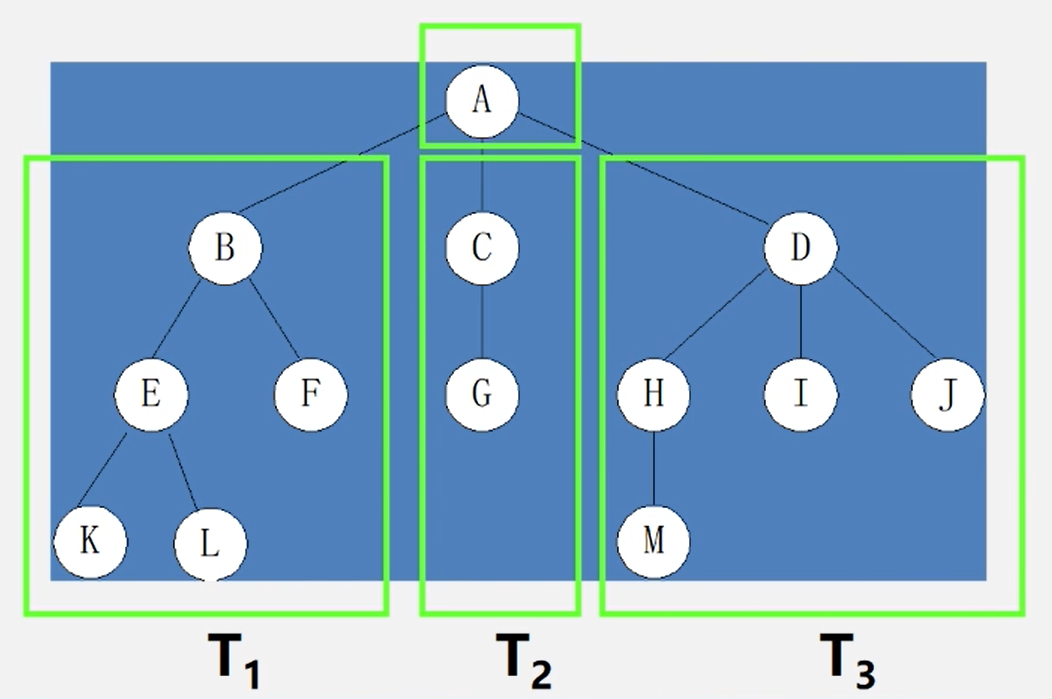
有且仅有一个特定的称为根(Root)的结点
其余结点可分为 m(m≥0)个互不相交的有限集 T1,T2,T3,…,Tm,其中每一个集合本身又是一棵树,并称为根的子树(SubTree)
由图可见,显然,树是一个递归的定义
0x04 树的基本术语
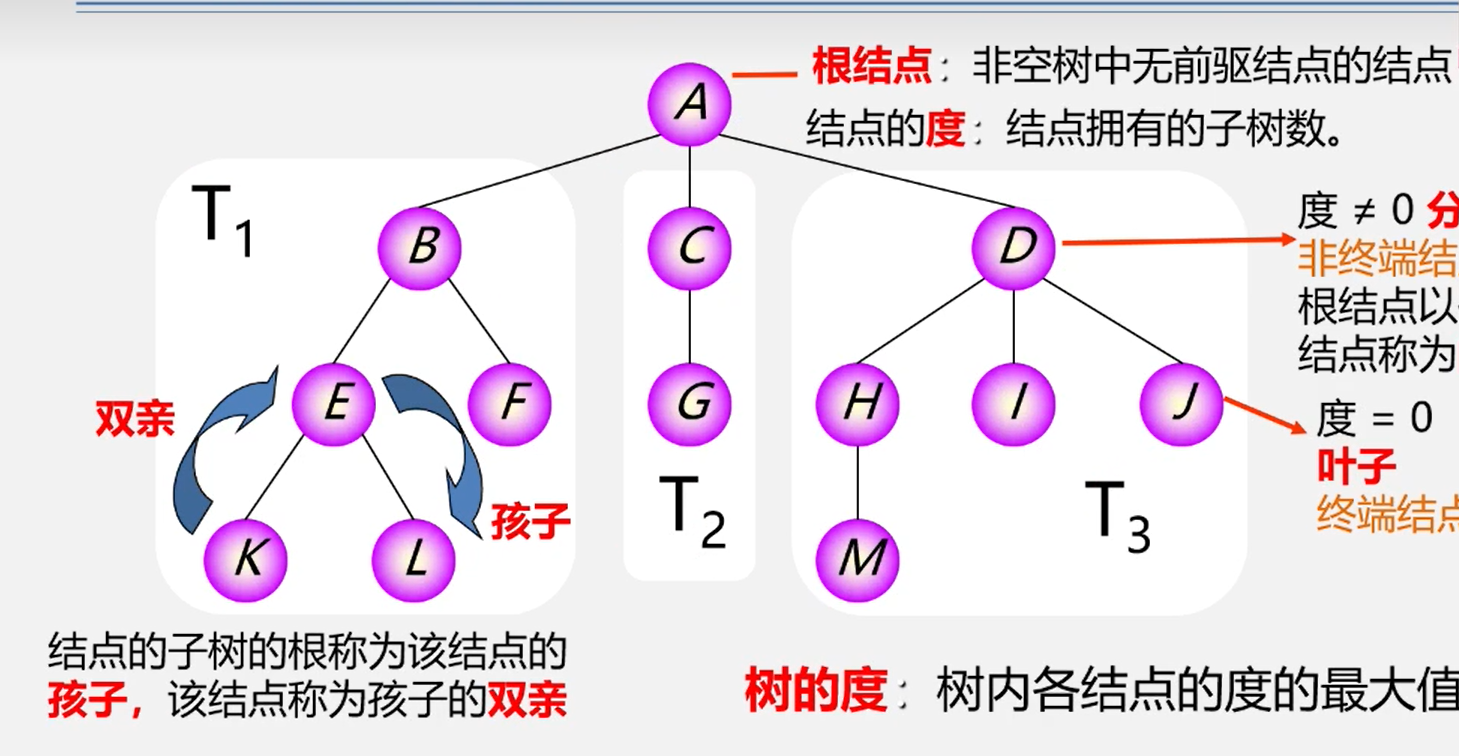
根结点:非空树中无前驱结点的结点(第一个)
结点的度:结点拥有的子树数
树的度:树内各结点的度的最大值
叶子:该结点的度为0,也叫作终端结点
分支结点:度不为0(非终端结点)
内部结点:根结点以外的分支结点
孩子和双亲:结点的子树的根称为该结点的孩子,该结点称为孩子的双亲
堂兄弟和兄弟:双亲在同一层的结点是堂兄弟,有同一个双亲的结点是兄弟
结点的祖先:从根到该结点所经分支上的所有结点
结点的子孙:以某结点为根的子树中的任一结点
树的深度(高度):树中结点的最大层次
森林:是m棵互不相交的树的集合,把根结点删除树就变成了森林,一棵树可以看成是一个特殊的森林,反过来,给森林的各子树加上一个双亲结点,森林就变成了树。
归纳得出,树一定是森林,森林不一定是树
0x05 二叉树的定义
为什么要研究二叉树
普通树(多叉树)若不转化为二叉树,则运算很难实现,因为
二叉树的结构最简单,规律性最强
可以证明,所有树都能转化为唯一对应的二叉树
二叉树的定义
二叉树是n(n≥0)个结点的有限集,它或者是空集(n = 0)或者由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二又树组成。
二叉树的特点
每个结点最多有俩孩子(二又树中不存在度大于 2 的结点)
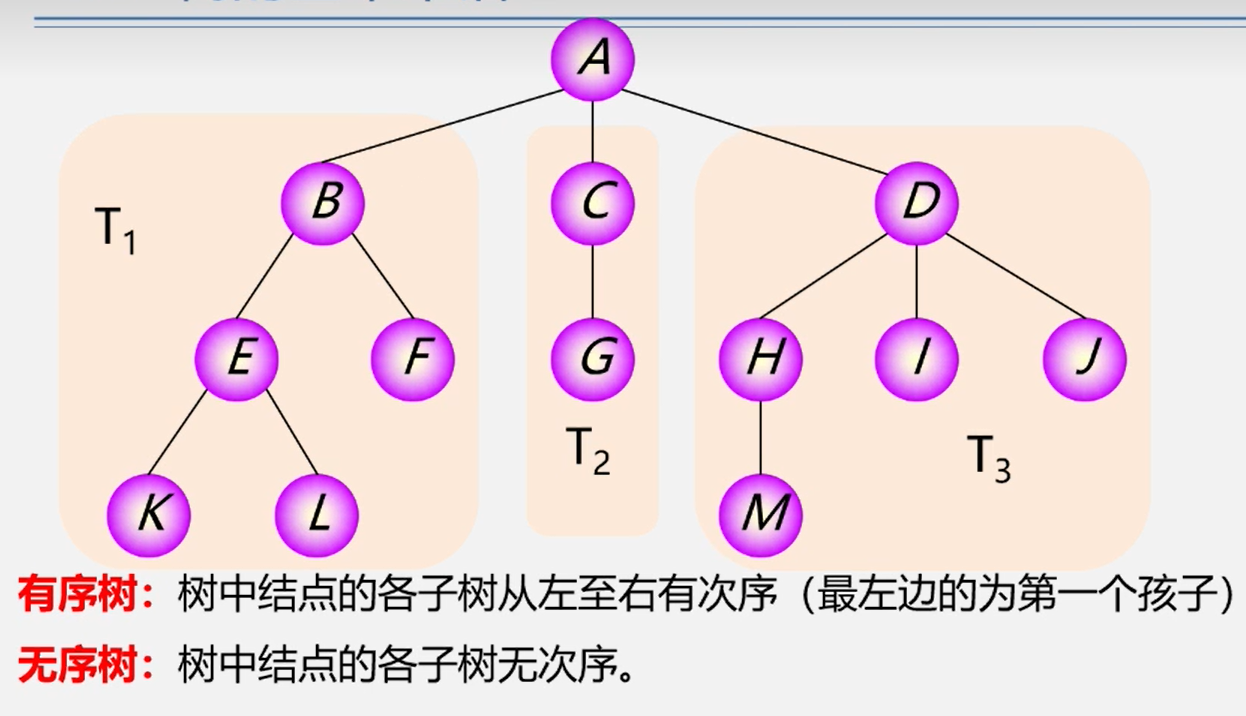
子树有左右之分,其次序不能颠倒。
二叉树可以是空集合,根可以有空的左子树或空的右子树
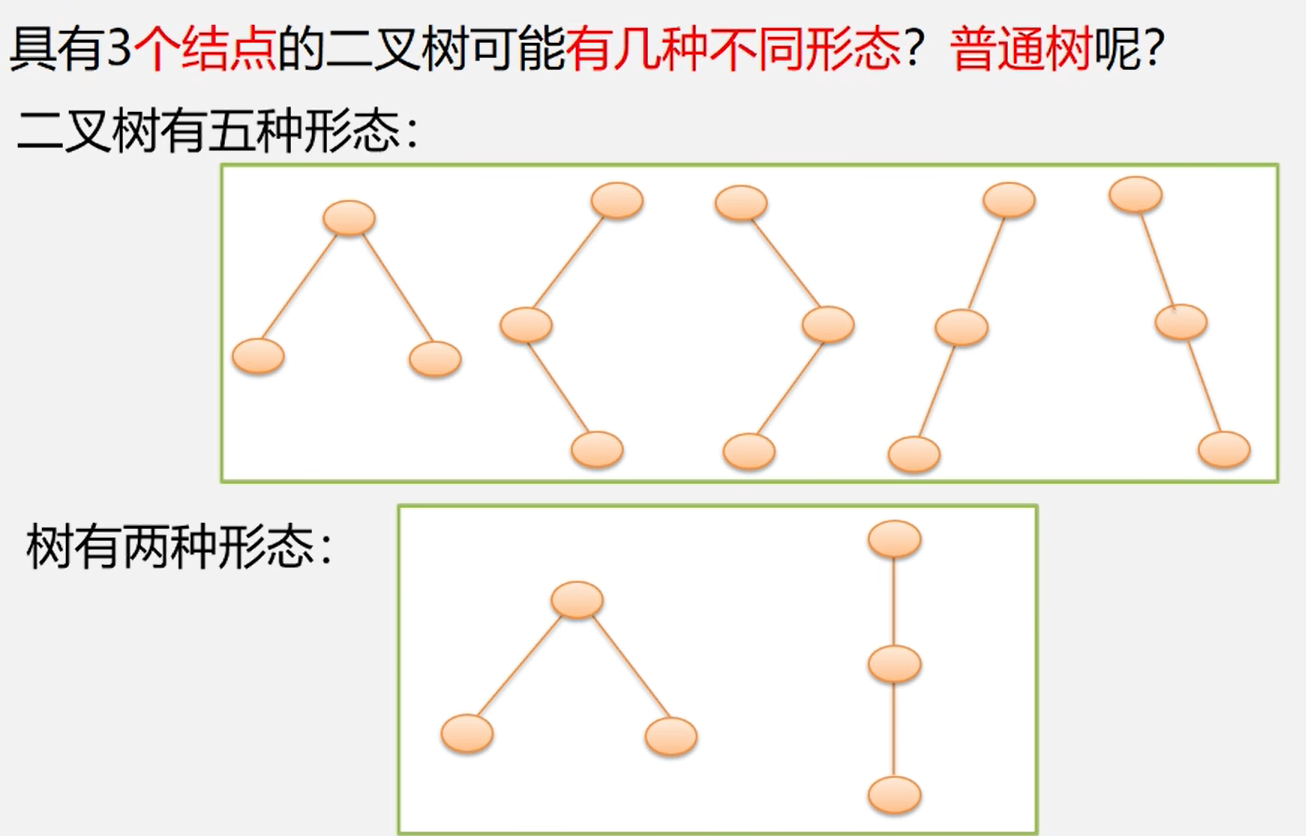
二叉树和树的区别
二叉树不是数的特殊情,他们是两个概念
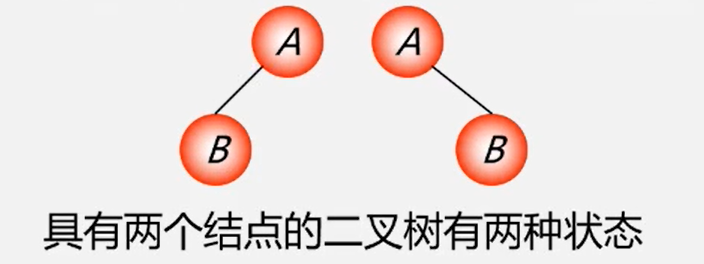
二叉树结点的子树要区分左子树和右子树,即使只有一颗子树也要进行区分,说明它是左子树还是右子树
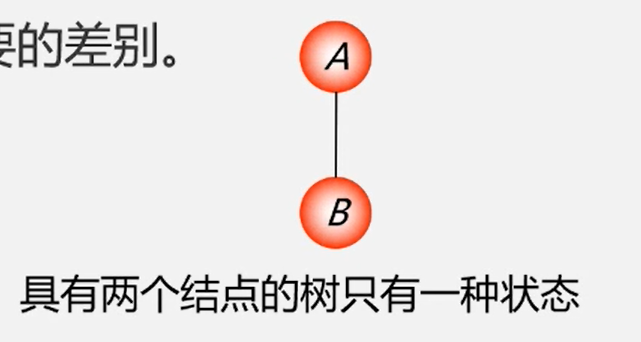
树当结点只有一个孩子时,就无须区分左右次序,这是二叉树和树最主要的区别。
也就是二叉树每个结点位置或者说次序都是固定的,可以是空,但是不可以说它没有位置,而树的结点位置是相对于别的结点来说的,没有别的结点时,它就无所谓左右了
0x06 二叉树的性质
三个普遍性质
性质1:在二叉树的第 i 层上至多有 2的i-1次方个结点(i>=1)
性质2:深度为k的二叉树至多有 2的k次方 - 1 个结点(k>=1)
性质3:对于任意一颗二叉树,如果其叶子数为n0,度为2的结点数为n2,则n0 = n2 + 1
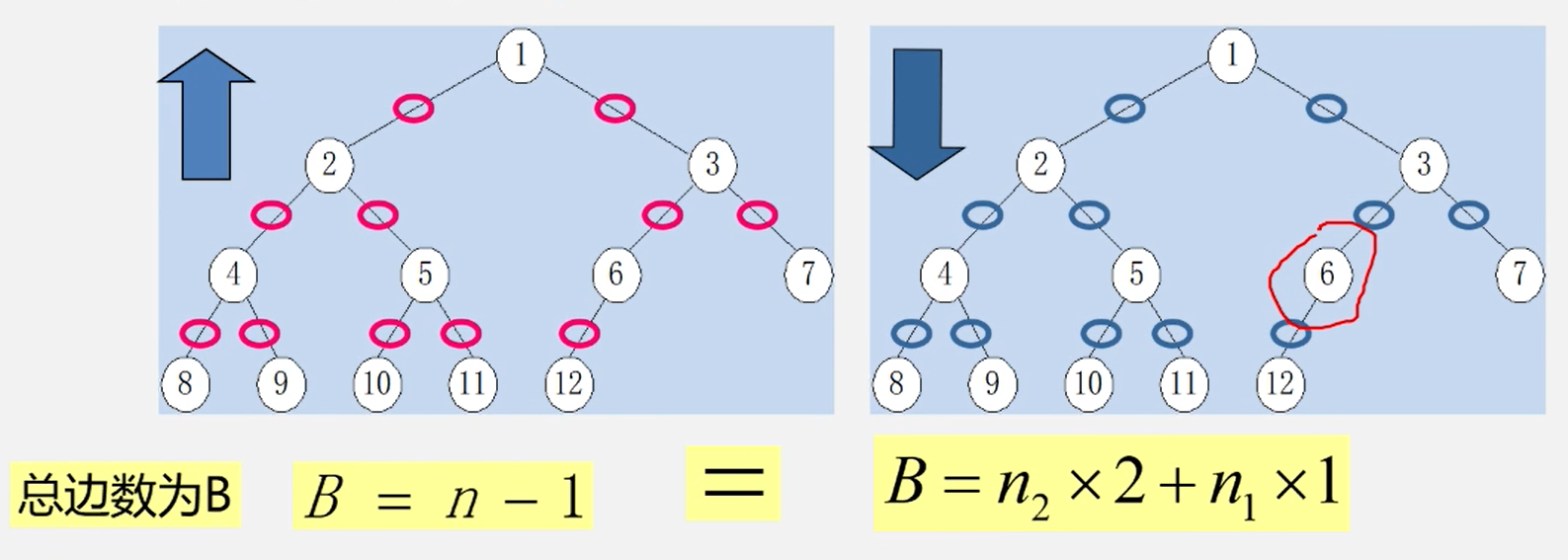
推导性质3:
每一个二叉树,记边数为B。
联立两个式子,n = 2 * n2 + n1 + 1,其中n = n0 + n1 + n2
化简得 n0 = n2 + 1
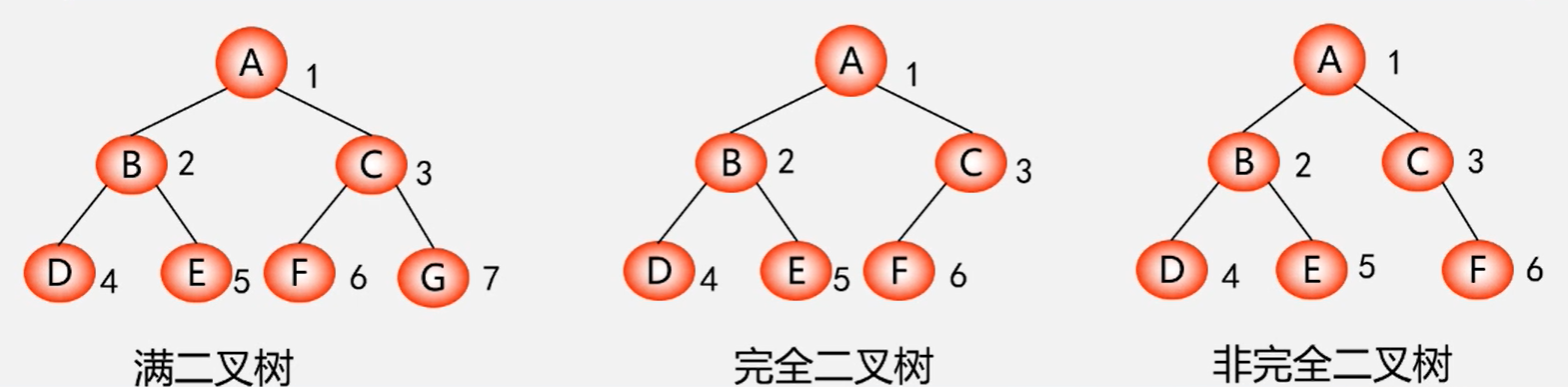
满二叉树
根据性质二,一颗深度为k且有2的k次方 - 1 个结点的二叉树称为满二叉树
特点:每一层的结点数都是最大结点数,叶子结点全部在最底层(同一层)
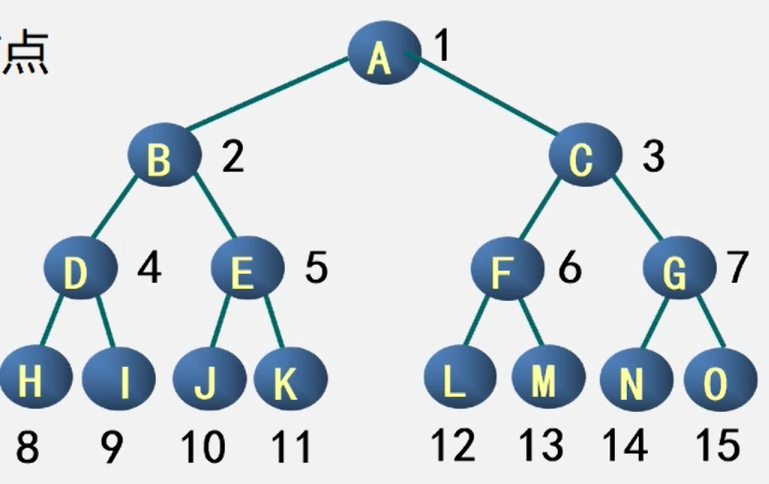
对满二叉树结点位置进行编号,从根结点开始,从上到下,从左到右,每一个结点位置都有元素。
完全二叉树
深度为k的具有 n 个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时,成为完全二叉树。
叶子只可能分布在层次最大的两层上。对于任一结点,如果其右子树的最大层次为 i ,则其左子树的最大层次必定为 i 或 i + 1 。
完全二叉树的性质
性质4:具有n个结点的完全二叉树深度为[log2 n] + 1 ([ ]是高斯函数)
性质4表明了完全二叉树结点数n与深度k的关系
性质5:如图,阐述了完全二叉树中双亲结点编号与孩子结点编号之间的关系